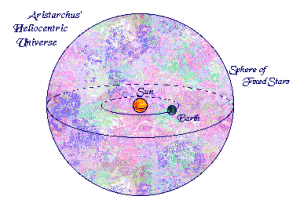
 L’ipotesi di Aristarco di Samo (III sec. a. C.) è nota: egli suppone che i pianeti compiano le loro rivoluzioni intorno al Sole (eliocentrismo) e non intorno alla Terra (geocentrismo); tale ipotesi (o supposizione) “salva i fenomeni”, dal punto di vista matematico in modo molto più semplice (ma non più preciso!) dell’ipotesi geocentrica secondo la quale tutti gli astri girerebbero intorno alla Terra, immobile al centro dell’universo; ipotesi quest’ultima, sistematizzata da Eudosso e Aristotele (IV sec. a. C.), quindi da Tolomeo, che da un lato meglio sembrava corrispondere all’esperienza dei sensi, dall’altro lato costringeva a elaborare complesse ipotesi supplementari su misura (o ad hoc) per spiegare i moti apparentemente irregolari dei pianeti sulla volta celeste.
L’ipotesi di Aristarco di Samo (III sec. a. C.) è nota: egli suppone che i pianeti compiano le loro rivoluzioni intorno al Sole (eliocentrismo) e non intorno alla Terra (geocentrismo); tale ipotesi (o supposizione) “salva i fenomeni”, dal punto di vista matematico in modo molto più semplice (ma non più preciso!) dell’ipotesi geocentrica secondo la quale tutti gli astri girerebbero intorno alla Terra, immobile al centro dell’universo; ipotesi quest’ultima, sistematizzata da Eudosso e Aristotele (IV sec. a. C.), quindi da Tolomeo, che da un lato meglio sembrava corrispondere all’esperienza dei sensi, dall’altro lato costringeva a elaborare complesse ipotesi supplementari su misura (o ad hoc) per spiegare i moti apparentemente irregolari dei pianeti sulla volta celeste.
Come si è giunti, dunque, alla scoperta dell’eliocentrismo?
Una tappa intermedia fu rappresentata da Eraclide Pontico, discepolo di Platone, che, pur mantenendo la Terra al centro dell’universo, immaginò che Mercurio e Venere anziché girare intorno alla Terra, girassero intorno al Sole (e, ovviamente, insieme al Sole, intorno alla Terra). Le anomalie di Marte restavano tuttavia inspiegate. Il modello che ne risultava è, salvo determinazioni quantitative che saranno assai più precise, quello che verrà sostenuto nel XVI secolo da Tycho Brahe.
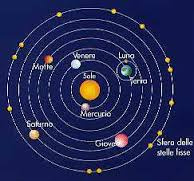 Fu per risolvere il groviglio di difficoltà proposto dai sistemi geocentrici che Aristarco di Samo propose, dunque, con un colpo di genio, il modello eliocentrico, che coincide puntualmente con quello proposto 18 secoli dopo da Copernico. il quale nel 1543 esporrà la sua dottrina nel testo De revolutionibus orbium coelestium (Sulle rivoluzioni dei pianeti).
Fu per risolvere il groviglio di difficoltà proposto dai sistemi geocentrici che Aristarco di Samo propose, dunque, con un colpo di genio, il modello eliocentrico, che coincide puntualmente con quello proposto 18 secoli dopo da Copernico. il quale nel 1543 esporrà la sua dottrina nel testo De revolutionibus orbium coelestium (Sulle rivoluzioni dei pianeti).
La riscoperta della dottrina di Aristarco permetterà infatti a Copernico di risolvere (“a tavolino”, ossia senza ricorrere a particolari osservazioni empiriche) in modo brillante ed elegante (dal punto di vista matematico) i problemi e le aporie del sistema aristotelico-eudossiano, nonché di quello di Tolomeo.
Nel modello copernicano, come in quello di Aristarco, i problemi del sistema aristotelico sono risolti come segue. Se il Sole è immobile al centro del sistema, i pianeti e la Terra possono finalmente muoversi di moto uniforme lungo orbite perfettamente circolari, senza le complicazioni introdotte dalle sfere aristoteliche e dagli epicicli tolemaici (cronologicamente successivi).
Con singolare parallelismo Archimede, operante nel III sec. a. C., (con la scoperta del principio che porta il suo nome, relativo al galleggiamento dei corpi), e Aristarco anticipano, dunque, la rivoluzione scientifica dell’età moderna, il primo nell’ambito della fisica, il secondo dell’astronomia. Si ha l’impressione che la scienza moderna non fece che riprendere un discorso rimasto misteriosamente interrotto nel III secolo a.C. Ad Aristarco (nato intorno al 310) si devono anche i primi tentativi di stabilire le distanze della Luna e del Sole, che portarono tuttavia a risultati inattendibili. Analoghe misurazioni furono fatte successivamente da Ipparco e da Posidonio, che riuscirono a calcolare la distanza della Luna con un errore del 20%, mentre per la distanza del Sole l’errore rimase assai superiore (60%).
Tuttavia anche il modello aristarcheo-copernicano presenta problemi per quanto riguarda la sua capacità di “salvare i fenomeni”.
- Come dimostrerà Keplero nel XVII sec., sulla base delle attente osservazioni di Tycho Brahe, se dobbiamo salvare i fenomeni fino in fondo, non possiamo ammettere che le orbite dei pianeti siano circolari. Esse devono essere ellittiche (il che riproporrà il problema della necessità di supporre forze di attrazione e repulsione, se ammettiamo, come fanno ancora Copernico e Galileo che il moto circolare uniforme sia naturale). Dunque il modello di Aristarco-Copernico non salva adeguatamente i fenomeni; addirittura lo fa in modo meno efficace del sistema tolemaico, così come fu perfezionato nel corso dei secoli.
- Nel modello di Aristarco-Copernico, il moto annuale della Terra intorno al Sole dovrebbe generare una variazione periodica dell’angolo di parallasse tra la Terra e due stelle fisse scelte a piacere sulla superficie del firmamento, ossia la distanza apparente tra le stelle dovrebbe variare al mutare della posizione della Terra nel suo moto di rivoluzione intorno al Sole; variazione di parallasse che però non si osserva. Per l’esattezza, se la distanza tra la Terra e le stelle fosse corta come il modello di Aristarco-Copernico prevedeva (presupponendo la finitezza del cosmo), il moto di rivoluzione della Terra intorno al Sole dovrebbe modificare ogni sei mesi l’ampiezza relativa dell’angolo formato dalle stelle tra loro e con la Terra (parallasse): avvicinandosi alla Terra le stelle di un emisfero celeste dovrebbero apparire più vicine e, per effetto prospettico, quasi “dilatarsi” rispetto a quelle dell’emisfero opposto, che dovrebbero quasi “restringersi”. L’assenza di questo fenomeno dimostra o che la Terra è immobile al centro dell’universo, secondo l’ipotesi geocentrica, o che le stelle sono molto lontane (al limite: a distanza infinita) e la variazione di parallasse risulta pertanto impercettibile (secondo quello che sappiamo noi oggi).
- Il moto della Terra intorno al proprio asse dovrebbe essere percepito dagli uomini: a) dovrebbe spirare un forte vento nella direzione opposta al moto della superficie terrestre, trascinando con sé tutti i corpi mobili (noi lo dovremmo percepire come percepiamo un vento apparente quando ci muoviamo su un carro o su una nave in una certa direzione); b) un oggetto lasciato cadere dall’alto dovrebbe descrivere una traiettoria obliqua in direzione opposta a quella del moto della Terra.
Le obiezioni scientifiche rivolte al modello eliocentrico nel mondo antico erano né più né meno che quelle addotte nell’età moderna contro Copernico e Galileo: in parte di natura geometrica, in parte di natura fisica.
Per quanto riguarda il problema della parallasse, va detto che in realtà una minima variazione di parallasse si registra, ma a causa della distanza delle stelle essa è rilevabile solo con strumenti molto raffinati e verrà misurata per la prima volta solo nel 1838 dal Bessel; anzi, la misura della variazione di parallasse è appunto il mezzo attraverso il quale si valuta la distanza delle stelle più prossime alla Terra (1 parsec, cioè un secondo di parallasse, equivale a circa 3,3 anni luce). La vera soluzione del problema implicherà l’adozione di un modello di universo infinito (nel quale le stelle possono essere collocate a enorme distanze dalla Terra).
Per quanto riguarda la mancata percezione del moto rapidissimo della Terra, richiesto dalla teoria eliocentrica, che dovrebbe anzi produrre su di noi effetti catastrofici, sarà Galileo, mediante una prima formulazione del principio di inerzia, a fornire un parziale chiarimento al problema.
Nonostante tutto questo, anzi proprio alle luce di questi sviluppi, possiamo apprezzare l’importanza dell’ipotesi eliocentrica di Aristarco, che sarebbe stata ripresa da Copernico.
In primo luogo essa resta di grande valore epistemologico (nel campo della filosofia della scienza) perché sottolinea il metodo adoperato dai “matematici” Greci, consistente nel formulare ipotesi, spesso francamente inverosimili (contrarie all’esperienza dei sensi), allo scopo di “salvare le apparenze” (i fenomeni) ricorrendo a modelli matematici semplici.
In secondo luogo sappiamo per certo che Copernico attinge alle fonti greche nell’elaborare il suo sistema, sicché sarebbe francamente ingeneroso considerare quella di Aristarco soltanto una “curiosa anticipazione” della teoria copernicana.
Quella di Aristarco, inoltre, non fu un’ipotesi che venne così presto dimenticata, come a volte si legge, a vantaggio delle teorie geocentriche di Aristotele e Tolomeo. Infatti la citano ancora, tra gli altri, autori tardi come Plutarco e Simplicio.
Ma è ancora più interessante la congettura di Lucio Russo, secondo cui il sistema eliocentrico era talmente noto presso i “matematici” greci da indurre Archimede di Siracusa, che certamente conosceva la teoria di Aristarco, citandola nel proprio Arenario, a costruire un vero e proprio modello di esso, in forma di planetario. La congettura si basa sulla seguente testimonianza di Cicerone:
L'invenzione di Archimede è da ammirarsi in quanto egli aveva escogitato in qual modo una sola "conversione" potesse riprodurre i diversi e vari percorsi, con moti tra loro contrastanti.
Russo ha buon gioco ad argomentare che questa “conversione” o rivoluzione non poteva che essere quella dei pianeti intorno al Sole, dal momento che per costruire un planetario geocentrico, peraltro molto più macchinoso e di dubbia realizzabilità, si sarebbero dovute progettare molte più “conversiones” (corrispondenti agli eccentrici e agli epicicli del sistema tolemaico o alla sfere celesti del sistema aristotelico).
Le notizie relative alla costruzione di altri planetari in epoche successive suggeriscono a Russo che il modello eliocentrico, almeno come ipotesi matematica, non sia stato abbandonato tanto presto.
Infine, ci dobbiamo chiedere: “Perché Copernico e, dopo di lui, Bruno e Galileo (così come prima di lui Archimede e Aristarco), insistettero tanto a difendere il sistema eliocentrico, nonostante le valide obiezioni che gli venivano opposte?”.
Certamente lo fecero per risolvere i problemi proposti dai modelli geocentrici, ma soprattutto perché, come sappiamo, tale modello obbediva a esigenze estetiche (di semplicità ed eleganza) e filosofiche (poneva il Sole al centro, simbolo del Principio in “Ermete Trismegisto”, nel mito della caverna di Platone ecc.).
Ad analoga esigenze “pitagoriche” obbediva, ad esempio, l’errata ipotesi di Keplero sulle orbite dei pianeti rispettivamente iscritte e circoscritte ai 5 solidi regolari di Platone, successivamente superata dalla corretta ipotesi relativa alle orbite ellittiche.
Sulla “rivoluzione copernicana” nelle sue conseguenze fino al processo di Galileo compreso cfr. questa puntata de Il tempo e la storia (Rai Storia).
astronomia, filosofia antica, filosofia moderna, fisica, matematica, scienza antica, storia dell'astronomia, storia della scienza
Archimede, Aristarco, Aristarco di Samo, Copernico, eliocentrismo, Eraclide Pontico, ipotesi eliocentrica, Keplero, orbite circolari, orbite ellittiche, sistema copernicano, Tycho Brahe
